(10)
|
Bulletin of TICMI |
15 |
Lemma 2. If the solution of problem (1)-(8), where
(10) |
|
u0(x) is consistent with the solution of (1)-(4) at t=0 on (x2,x1), (11)
exists, then it is unique.
For construction of a solution we use an idea of Schwartz alternating iteration method, which reduces the coupled problem to the sequently solving of boundary value problems. Corresponding boundary conditions at n-th iteration have the following form:
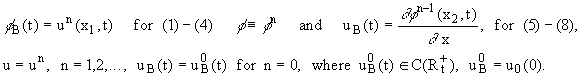
Lemma 3. If 
and f(x,t) satisfy conditions
(12) | |
|
+k q ,x) | £1/k2 |
for any |  |
(13) |
| f(t+k q ,x) | £1/k2 |
for any |  |
the sequences un and f n constructed by means of the above iteration method converge uniformly.
Theorem. If 
and f(x,t) satisfy (12) and (13) correspondingly then the solution of the problem (1)-(8), (10), (11) exists and is unique.
ON A UNIQUENESS OF THE SOLUTION OF INVERSE
PROBLEM FOR POTENTIAL THEORY
D.W. Kapanadze
Institute of Geophysics
Georgian Academy of Sciences
Solution of the inverse problem for potential theory is of a great theoretical and practical importance. A charachteristic feature of the multidimensional inverse problems is their incorrectness by Hadamard. The central point in the theoretical investigation of incorrect by Hadamard problems is the proof of the uniqueness theorem.
In the sequel W is a piece-wise smooth domain in R2. We denote by W ¥ a connected component of R2 /
such that ¥ Î W ¥ .
Theorem 1. Let W 1,
W 2
be piece-wise smooth, bounded, simply-connected domains in
R2, W =W
1È W 2.
Let us assume that there exists an neighbourhood
s or={x:|v-xo| < r}
Ç ¶
W ¥ of the point
xo Î ¶
W ¥ such that 
. Further let the neighbourhood s or contain a segment
