(9)
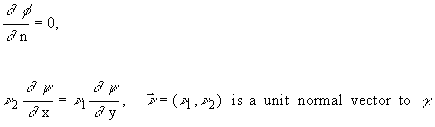
|
Volume 1, 1997 |
12 |
constructed by means of coupling of corresponding vortical and potential solutions if and only if on interface boundary the following conditions are satisfied:
| (8)
(9) |
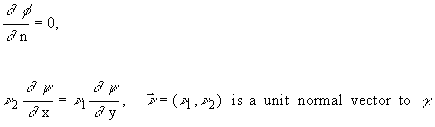 |
5. Resulted boundary value problems. Let suppose that ![]() satisfies Zommerfeld's boundary conditions at infinity if
satisfies Zommerfeld's boundary conditions at infinity if ![]() is an outer domain and
is an outer domain and ![]() vanishes at infinity if
vanishes at infinity if ![]() is an outer domain. With account of this for
is an outer domain. With account of this for ![]() we derive Laplace equation with standard Neuman's boundary condition and we have (3), (9) for
we derive Laplace equation with standard Neuman's boundary condition and we have (3), (9) for ![]() .
.
6. Remarks. Evidently the developed approach enables to construct variety of certain weak discontinuous solutions for (1),(2). Especially it may be useful for a construction of various soliton type solutions. We suppose that the approach is useful in the sense that it leads to several new and unexplored problems.
MIXTURE OF ELASTIC SOLID AND VISCOUS FLUID
G. Chichua
I. Vekua Institute of Applied Mathematics,
I. Javakhishvili Tbilisi State University
This paper deals with study a boundary-contact problem with unilateral contact conditions for the mixture of elastic solid and viscous fluid (see [1]). The solution has been defined as solution of the following variational inequality:
(1) (r u''(t), v-u'(t))+a(u(t), v-u'(t))+b(u'(t), v-u'(t))³ (f(t), v-u'(t)), " vÎ K
where u, u'Î L¥ (O,T;V), u''Î L¥ (O,T;H), u'(t) Î K,
V:={u; uiÎ H1(W ); ui |¶ W =0},
K:={u; uÎ V; [ui Ni] ³ 0 a.e. on å },
The solution of (1) has been approximated by means of characteristic functions. The following scheme of approximation has been built: find u2,u3,...,un, such, that
(2) (r g i, v-di)+a(ui+1, v-di)+b(di, v-di) ³ (fi, v-di) (i ³ 1), " vÎ K, diÎ K.