(3) u ⁰=u¹=0.

The stability, weak and strong convergences have been proved.

R e f e r e n c e s

[1] G. Chichua, On a Boundary-contact Problem for a Solid-Fluid Model, Reports of Enlarged Session of the Seminar of I. Vekua Institute of Applied Mathematics, 1995, v. 10, N1, 18-20 pp.

INVESTIGATION AND NUMERICAL SOLUTION OF ONE

INITIAL-BOUNDARY VALUE PROBLEM FOR

CHARNEY REGULARIZED EQUATION

In the cylinder Q=W x(0,T), where W is a rectangle {(x,y):0<x<l₁, 0<y<l₂} with the boundary ¶ W and T is a positive real number, there is considered the following initial-boundary value problem:

(1)

  (2)   U(x,y,t)=0, (x,y,t)Î ¶ W x[0,T],

  (3)   D U(x,y,t)=0, (x,y,t) Î ¶ W x[0,T],

  (4)   U(x,y,0)=U(x,y), (x,y)Î W .

Here D is the Laplace operator with respect to variables x,y, D ² =D D , J is the Jacobian, b ,v=const>0 and U₀ is a known function.

The equation (1) without the term vD ²U is called the Charney equation. Such a type of equations arises in the investigation of atmospheric motions. Note that (1) model some other physical problems.

Following to J.-L. Lions the existence and uniqueness of the solution of the problem (1)-(4) is proved.

It is also investigated the difference scheme

(5)

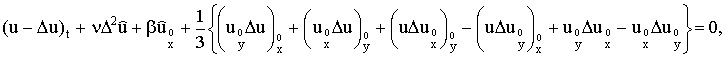  (6)   u(x,y,t)=0, (x,y,t)Î ¶ w x w t ,

  (7)   D u(x,y,t)=0, (x,y,t)Î ¶ w x w t ,

  (8)   u(x,y,0)=U₀(x,y), (x,y)Î v .