|
Bulletin of TICMI |
11 |
ABSTRACTS OF MINISIMPOSIUM
1996
ON A CONSTRUCTION OF DISCONTINUOUS SOLUTIONS FOR EQUATIONS
OF IDEAL LIQUID USING COUPLED VORTICAL AND POTENTIAL FLOW MODELS
R. Bochorishvili
I. Vekua Institute of Applied Mathematics
I. Javakhishvili Tbilisi State University
1. Stationary equations of ideal liquid in two space dimensions.
| (1) |
| (2) |
where P is a pressure,
![]() =(u1,u2)T is a velocity vector,
=(u1,u2)T is a velocity vector, ![]() =const.
=const.
2. Regularity requirement and simplified models. It is well known that under requirements ![]() ,P Î C2 the system (1),(2) can be reduced to linear equations. Namely in the case of vortical flow, i.e. rot
,P Î C2 the system (1),(2) can be reduced to linear equations. Namely in the case of vortical flow, i.e. rot![]() ¹ 0 , (1),(2) can be reduced to the following system
¹ 0 , (1),(2) can be reduced to the following system
| (3) |
![]() is stream function,
is stream function,
| (4)
(5) |
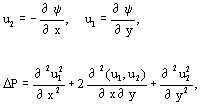 |
or in the case of potential flow, i.e. rot = 0,
to the Laplase equation
= 0,
to the Laplase equation
| (6) |
![]() is a potential function,
is a potential function,
| (7) |
but Poissons equation for pressure is the same as (5).
3. Formulation of a problem. Let ![]() be a domain with sufficiently smooth boundary g . Let a flow be potential in
be a domain with sufficiently smooth boundary g . Let a flow be potential in ![]() and it be vortical in
and it be vortical in ![]() . Find out interface boundary conditions ensuring the solution constructed by coupling of solutions of corresponding simplified problems to be a weak discontinuous solution of(1),(2) in R2.
. Find out interface boundary conditions ensuring the solution constructed by coupling of solutions of corresponding simplified problems to be a weak discontinuous solution of(1),(2) in R2.
4. Interface boundary conditions. The system (1),(2) may have discontinuous weak solution